这一次,彻底弄懂七年级数学中【数轴上的动点问题】

数轴上的动点问题属于七年级上学期必考的压轴题型,这类题型基本上都是以数轴为载体,通过分类讨论来解决问题。
很多初一的小伙伴都觉得这类题很难,在答题的时候,要么找不到思路,要么分类讨论的时候特别容易漏解,所以本能的就会畏惧。
但考试当中,你想拿高分,这类题是必须要拿下的。
而事实上,只要掌握了方法,找到正确的解题思路,这类题也是一定可以拿下的。
首先,我们需要掌握【数轴上动点问题】基本答题策略(六步法)。
1. 画图打草稿——在数轴上表示出点的运动情况:包括点的运动方向和速度;
这一类题目的题干往往会比较长,而且涉及到的小问也会比较多,比如,图片中的这道题,它的题干信息量非常大,还有3个小问。

所以在读题的过程中,就要在数轴上标出题干里的重要的已知信息,这样才能方便后续结合数轴分析问题。
标记已知条件,这是一种方法,也是一个一定要养成的好习惯。
2. 表示动点——写出运动过程中动点表示的数:一般用含有t的代数式表示,向右运动用“+”表示,向左运动用“-”表示;
在数轴上分析问题,无外乎是关于点和线的左右移动,而涉及到“左”“右”,就需要考虑“+”“-”,涉及到移动,就会涉及到速度v和时间t,所以要掌握利用含有t的代数式来表示点在运动过程中所表示的数,并且要注意“+”“-”号的问题。
比如,下面这道题。
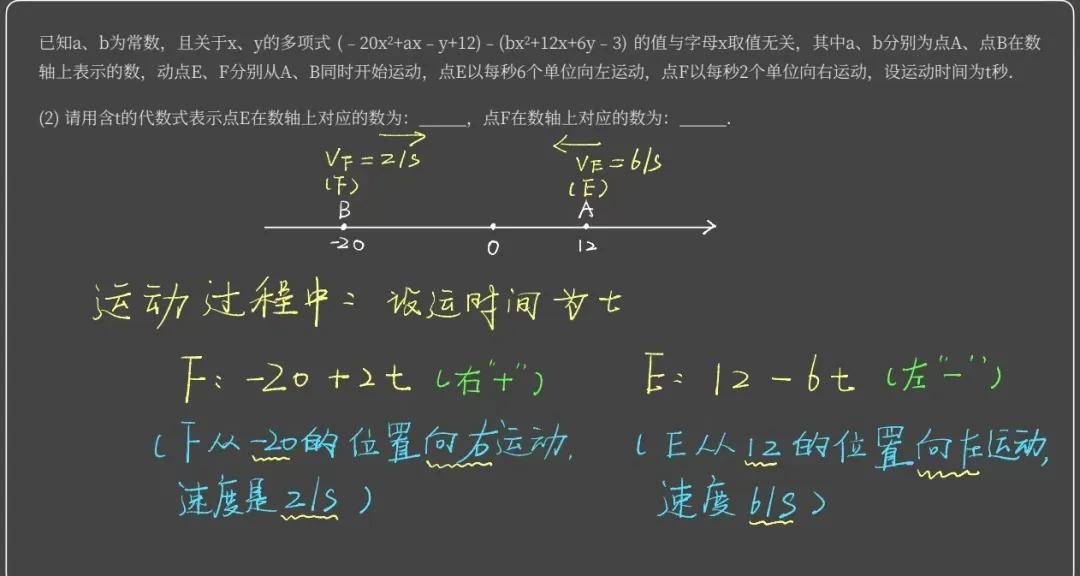
3. 表示距离/线段长度——利用点的代数式来表示点与点之间的距离:通过右边的点减去左边的点来表示数轴上两个点之间的距离,若无法判定两点的左右,那就需要加上绝对值“| |”;
比如,这道题,要求运动过程中E、F的距离,因为在运动过程中,E、E的相对位置会发生变化,所以我们给表示EF距离的表达式套上一个绝对值。

4. 表示关系/列方程——根据条件列方程或代数式,求值:当我们把前面三步准备工作做好,接下来就可以结合题目当中所给的已知条件建立方程,求解。这一步的关键,在于要算对。
5.解绝对值方程
在这里很多情况下都会涉及绝对值方程,所以还要学会解绝对值方程。数轴动点中常见的三类绝对值方程的解法(看下图)。
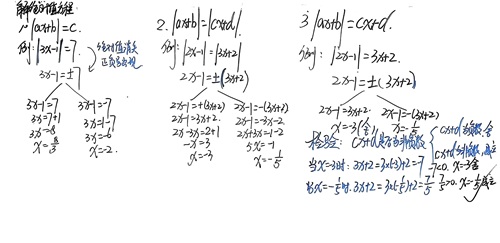
6. 舍值——舍去不符合题目要求的答案。很多情况下求出来的可能有多个答案,有时候也要考虑是否舍值。一般需要舍值情况有:时间为负数,时间超过最大限值(比如题目要求谁先到达就结束运动,就隐含有时间的限值)
以上就是处理【数轴上动点问题】的六个基本步骤,非常清晰非常通用,掌握好也不困难,你要记好。
当然,对于这类问题来说,真正困难的,也是考察的核心点:在答题的时候,如何进行有效的分类讨论。但是要注意的是使用绝对值可以替代分类讨论,所以熟练掌握绝对值的相关知识对数轴动点的学习也非常重要。
复杂的动点问题,往往有很多种情况,如果你分类讨论的依据没有建立好,那么就极有可能会漏解。
想要把这一步做好,就只有一个字,练。
当你把三五个题型一总结,那基本的答题框架就清晰了,并且,通过刻意的练习还可以不断强化我们思维的缜密性,避免出现漏解扣分的情况。
未来的学习当中,我们会面临更复杂的动点问题,所以一定要从初一就开始建立自己思考问题的体系。
