线性代数的秘密:什么是线性相关和线性无关
线性代数里面的线性相关和线性无关究竟是什么?
话不多说,让我们开门见山:
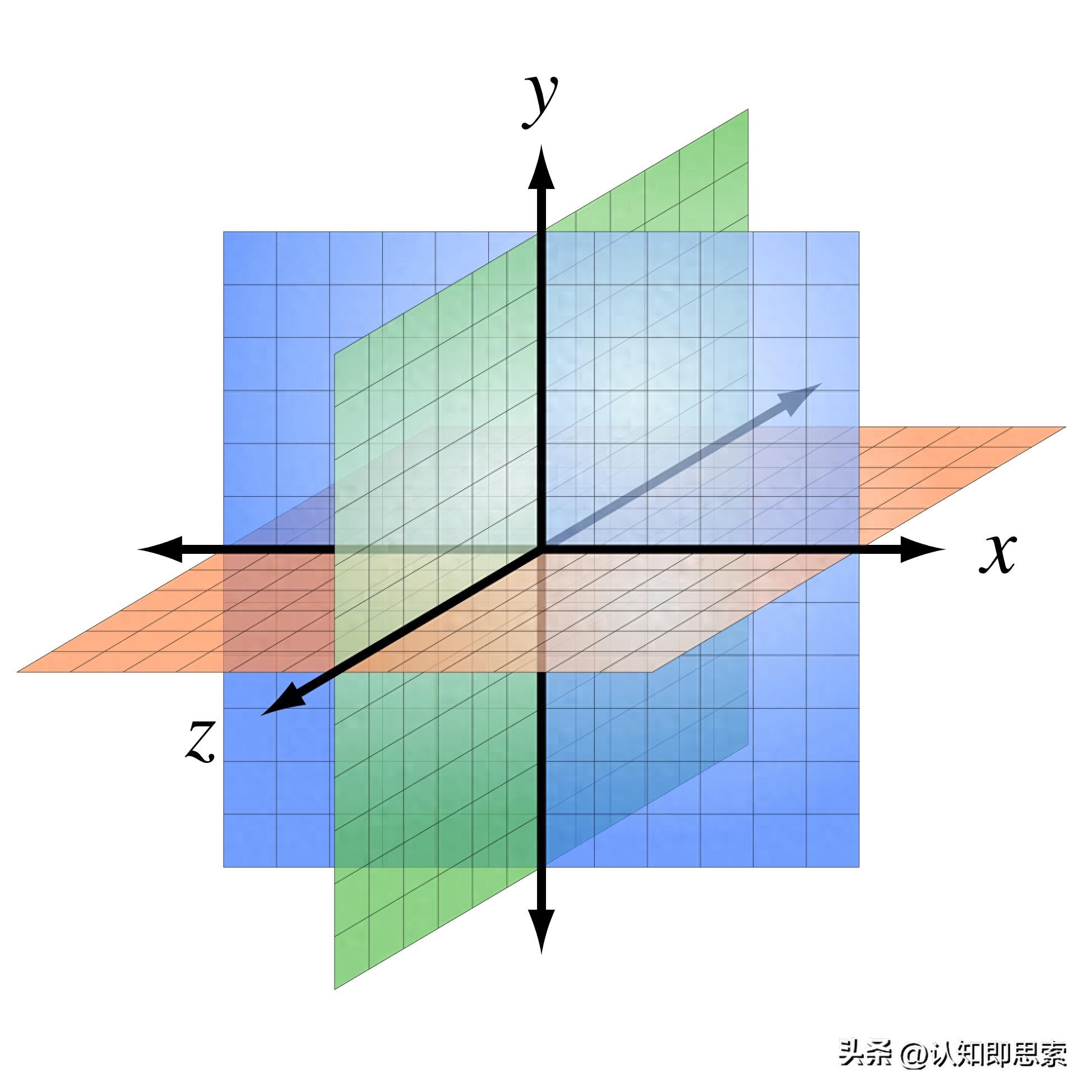
先说线性无关
我先不告诉你们线性无关的定义是啥,首先我们看一下欧几里得空间R中的三维直角坐标系xyz,三个基底矢量(1,0,0),(0,1,0)和(0,0,1),它们就是所谓的“线性无关”:
这三个基底向量可以写成:
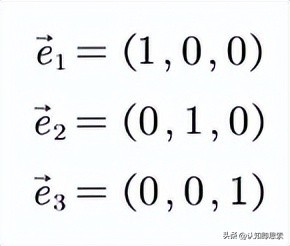
实际上,这三个基底向量张成的空间就是一个三维(正交)空间,这些基底向量处处都张成了直角,注意数形结合的思想去理解它:

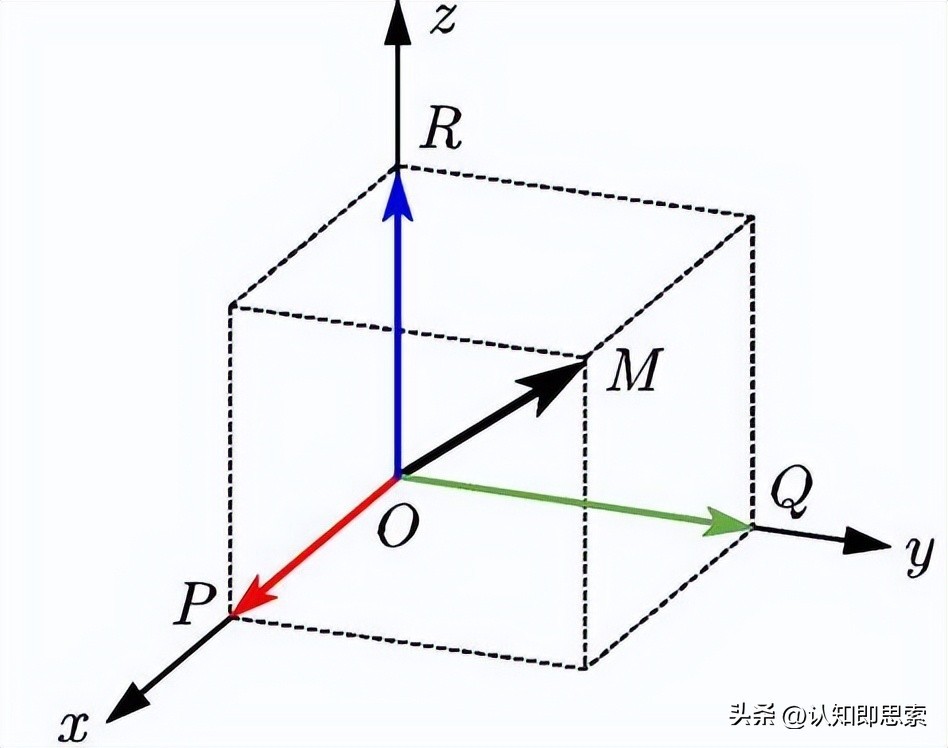
为啥它们“线性无关”呢?
1.很明显,一维人少了一个维度,它就不能理解二维人在做什么。二维人少了一个维度,它就不能理解三维人在做什么。
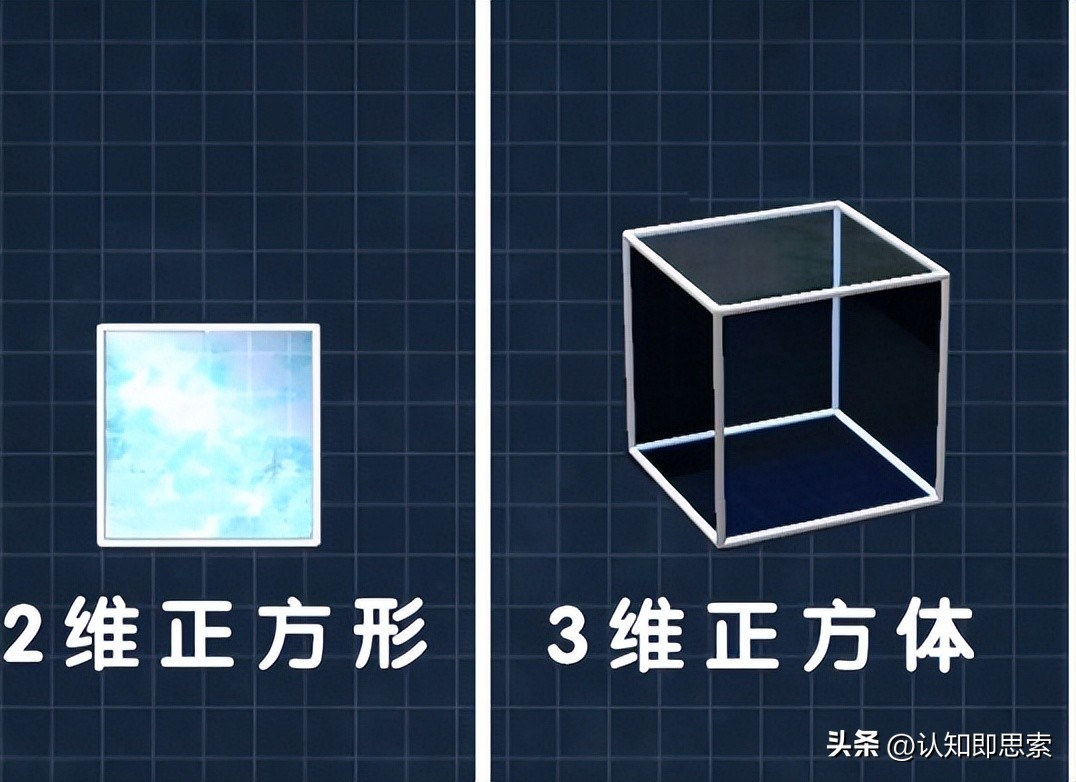
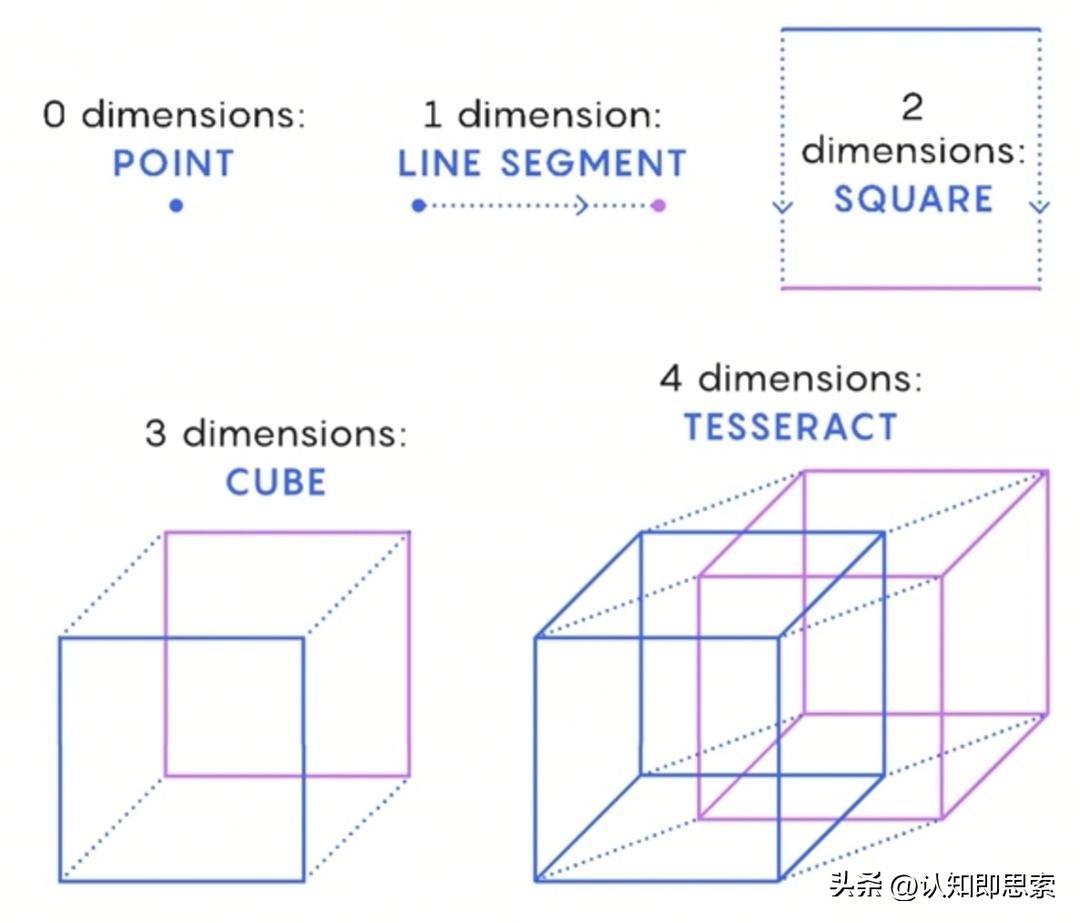
我们三维人正是因为缺少了(0,0,0,1)这个基底向量,所以没办法知道四维空间长什么样子:

四维超正方体在三维空间的投影
然而,我们却可以用数学的方式把这个四维正交空间表述出来,并研究它的性质:

可以看出,e1,e2,e3,e4之间都是互相线性无关的,因为它们代表着不同的维度,缺了谁都不好使,它们都是组成一个空间必不可少的基本因子。
什么是线性相关呢?
我们随便看个矩阵:
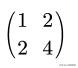
这个矩阵,乍一看上去能构成一个斜角坐标系,也就是基底i'=(1,2),j'=(2,4)的斜角坐标系,然而,当你实际去画的时候,发现这“矩阵”实际上只是一维坐标,因为这两个基底向量重合了,只是差了2倍:
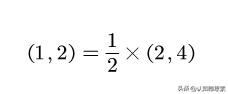
所以我们就说i'=(1,2)和j'=(2,4)这俩向量线性相关。再进一步,我们拿个三维空间里面随便两个向量a和b,只要你说:
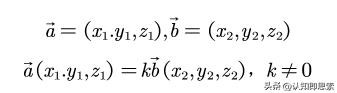
这两个向量就是共线的,它就是所谓的 “线性相关“。至于这个k是正还是负,是整数还是无理数,都无所谓,因为它们在一条线上。如果它们俩构成一个矩阵,那么自然要降低一个维度,也就是说该矩阵是“不满秩”的。(当然,如果你不理解什么是秩,那也没关系,本文并不打算讲清楚它)
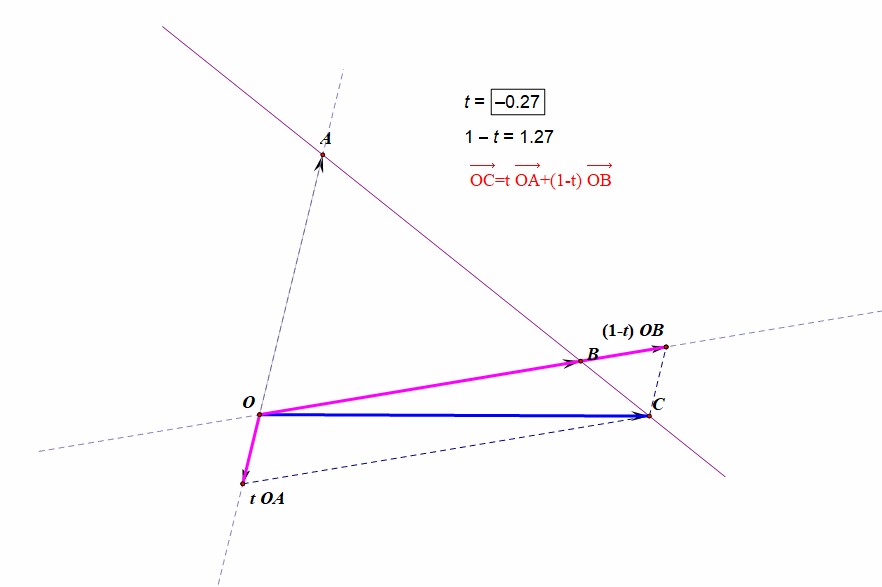
再举一个例子,比如下面这个矩阵,它的三个基矢量分别为(1,2,3),(2,4,6),(5,6,7),这乍一看上去是一个三维斜角坐标系,构成了一个斜空间,然而(1,2,3)=0.5倍(2,4,6),所以这俩向量线性相关,因而这个“三维斜角坐标系”的真面目只是“二维斜角坐标系”,你知道它是多少吗?

线性相关的物理意义
这里随口一提,线性相关主要体现在信号处理和系统分析等领域。在线性系统中,如果一个输入信号可以分解为多个独立的脉冲信号,那么这些信号就是线性相关的。例如,在音频处理中,如果两个频率之间存在整数倍的关系,那么这两个频率就是线性相关的,因为它们可以通过滤波器进行分离。
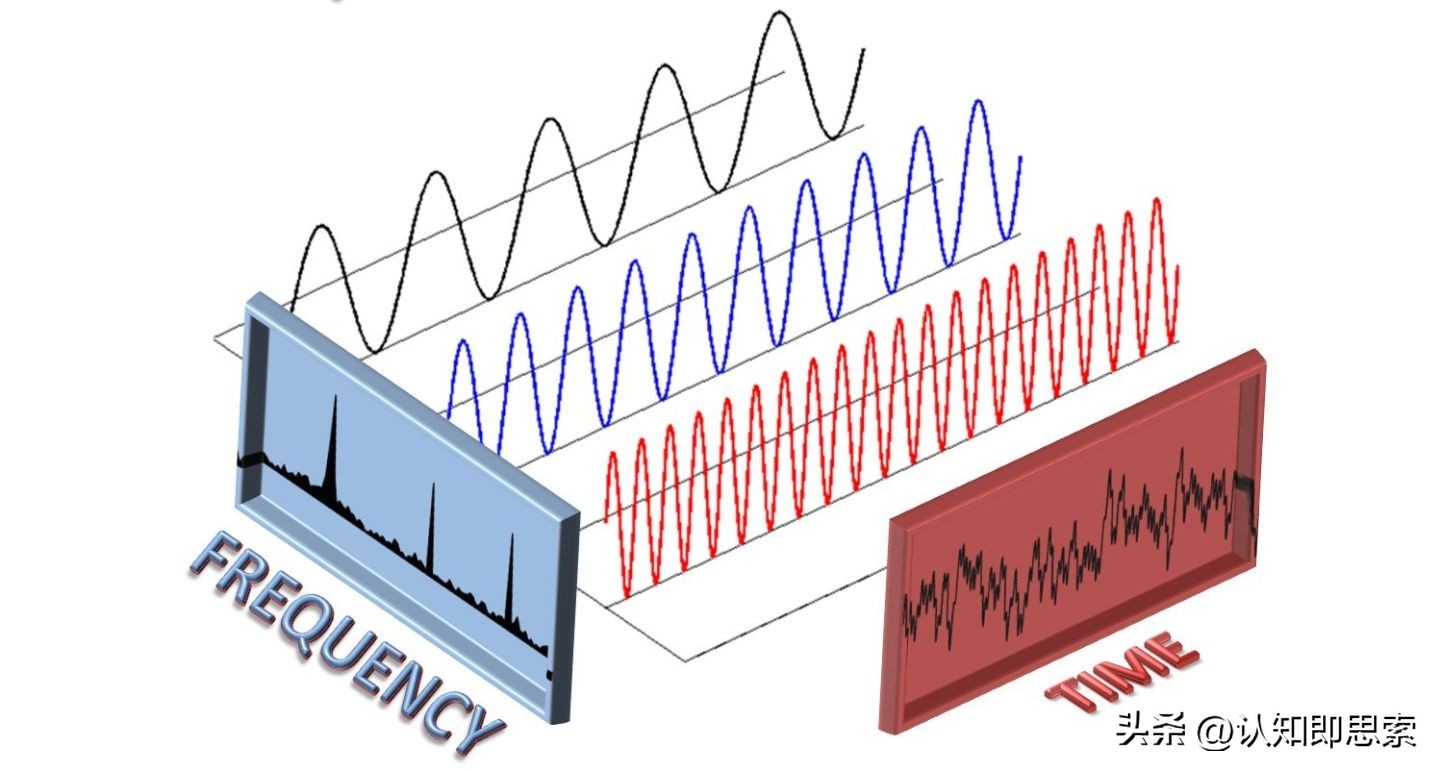
此外,线性相关的概念也常用于描述物理现象中的因果关系。例如,在物理学中,如果一个物体的运动状态可以由其他物体的运动状态线性组合得到,那么我们就说这两个物体是线性相关的。这种关系可以帮助我们理解和预测复杂的物理系统的行为。
你理解线性相关和线性无关了吗?欢迎在评论区留言。
